How to Call Out Bad Ideas
If you have ever been convinced of or swayed by some presentation of information that you later found out was BS, welcome to life. While BS has, in the last several decades, most prominently been spewed forth as corporate jargon or postmodern solipsisms, a new wave of BS now aggravates us and threatens our progress. This new kind of BS hides behind the language of mathematics, statistics, and science to construct an image of veracity.
Whereas old BS looked like this:
‘Our collective mission is to functionalize bilateral solutions for leveraging underutilized human resource portfolio opportunities.’ (corporate jargon meaning we are a temp agency)
And this:
‘Hidden meaning transforms unparalleled abstract beauty.’ (postmodern solipsism)
The new BS that is the topic of this article looks like this:
‘While short of statistical significance (p = 0.13), our results underscore the clinically important effect size (relative odds of survival at five years = 1.3) of our targeted oncotherapy and challenge the current therapeutic paradigm.’
As you can see, this claim and others like it create legitimacy by using numbers, statistics, and other veneers of rigor. But there are numerous assumptions and questions that are left unanswered. For example, we may ask: what is the justifiable relationship between statistical significance and clinical importance? Is five years a relevant time horizon for this cancer? What is the current therapeutic paradigm and why should this matter to the reader?
While old BS is probably never going to go away, this new BS merits our present attention because it is relatively difficult to refute; many of us do not feel qualified to question information that is presented in a quantitative or technical format. This is bad. We live in a world that is rife with BS. As college professors Carl T. Bergstrom and Jevin D. West put it,
Politicians are unconstrained by facts. Science is conducted by press release. Silicon Valley startups elevate bullshit to high art. Colleges and universities reward bullshit over analytic thought. […] Bullshit pollutes our world by misleading people about specific issues, and it undermines our ability to trust information in general.
Their book, Calling BS: The Art of Skepticism in a Data Driven World, is borne from their desire to help students navigate information and draws from a course fittingly titled ‘Calling BS ’ that they teach at the University of Washington. This article, in turn, is based on their book. The good news is that becoming better BS detectors and whistle-blowers do not require us to be statisticians or data scientists. For the most part, all that is required is some straightforward reasoning techniques and access to a search engine.
Before we get to the good part, let us anchor on a definition of BS. When someone is BS-ing, they are not communicating, they are manipulating, whether intentionally or not, and doing so with rhetorical flair, superfluous detail, or statistical falsehoods. Similarly, the definition offered by Bergstrom and West goes like this:
Bullshit involves language, statistical figures, data graphics, and other forms of presentation intended to persuade or impress an audience by distracting, overwhelming, or intimidating them with a blatant disregard for truth, logical coherence, or what information is actually being conveyed.
Tracing the Stench
BS has existed for as long as there have been brains. While it might seem especially pervasive today, it is not peculiarly modern. The Greek philosopher Plato complained over two thousand years ago that the Sophists, an intellectual school of thinkers, were only interested in winning arguments and not in discovering and championing the truth. But even before the advent of humanity, BS can be traced to deception among other animals in the animal kingdom which has been going on for millions of years.
Animals have evolved physical traits and behavioural responses to deceive and detect deception. This area of animal ecology is rather fascinating. For the most part, however, their behaviours are not particularly sophisticated.
They become more sophisticated the higher up the cognitive tree these animals reside. Once animals possess a theory of mind, controversial in most species except ours, they are able to think from the perspective of their mark, know what they do not know, and craft their BS accordingly. This is where BS can become endlessly complex and even pathological, especially when we factor in the power of complex communication systems such as human language augmented by technology. For example, a capuchin monkey can warn his friends of a predator through calls and may therefore leverage false alarms to steal their food when they flee from an imagined predator. Humans, by contrast, can craft successive emails soliciting money from vulnerable, distracted, or naïve individuals by convincing them that they are Nigerian princes, government authorities, and the like.
Some of the BS we create may not even be within our conscious awareness. We truly are an enigmatic lot.
To summarise, BS can be traced back to the beginning of life. Using an analogy from our modern economy, someone is always trying to sell us something. Add in the cognitive and linguistic tools that we possess, as well as the many incentives to do so, and BS multiplies. Hence it is little surprise that there are various kinds of BS, constructed to serve different purposes. For instance, sometimes misleading would be the better option than lying outright to preserve one’s reputation.
When Bill Clinton was subsequently called out on his claim that ‘there is no sexual relationship [with Monica Lewinsky],’ he responded by saying his statement was true because ‘is’ signifies the present tense, and when he was asked that question, he was no longer in a sexual relationship with her. Known also as paltering, these kinds of statements offer plausible deniability when used correctly, and it can preserve one’s reputation better than an outright lie would. It is, however, still BS because it was crafted to lead people away from the truth.
The amount of energy needed to refute bullshit is an order of magnitude bigger than [that needed] to produce it.
Alberto Brandolini, Software engineer
There is a mountain of evidence that refutes any causal connection between vaccines and autism. Yet, the anti-vaccine movement still persists. This is in part because of a study published in 1998 in The Lancet by Andrew Wakefield about the possible connection between autism and the MMR vaccine. Even though the study has already been discredited multiple times, its co-authors formally retracting their interpretations, and the article itself being removed from The Lancet, the movement it instigated still persists and has contributed to the resurgence of measles.
In 2010, Wakefield was found guilty of professional misconduct by the relevant authorities, and in 2011, the British Medical Journal editor-in-chief Fiona Godlee formally declared his original study to be a fraud with an intent to deceive because of the sheer incompetence evident in the study. To combat this, stalwart defenders of the anti-vaccine movement invented a story about big pharmaceutical companies conspiring to hide the truth from them. Hence, in spite of all the evidence against some causal connection between vaccines and autism, a portion of the public remain swayed by these fears.
A few characteristics we may glean form the above case study about BS is that (1) it takes less work to create BS than to clean it up, (2) it does not require as much intelligence to construct BS than to tear it down, (3) and it often spreads much faster than it can be corrected. Another example from social media and the 2013 Boston Marathon can serve to demonstrate the above three characteristics.
Soon after the terrorist bombing at the marathon, a story of an eight-year-old girl who was killed appeared on Twitter. Her story became viral because she had apparently been a student at Sandy Hook and was running in memory of her classmates who were killed in the mass shooting that had occurred there only recently. Thousands who saw the tweet responded with grief and compassion. But some who questioned the story noted that the Boston Marathon did not allow children of that age to participate, and that the bib she was wearing pointed to a different race. After corroborating the facts, it was determined that the girl had not, in fact, been killed. Twitter users sent out more than two thousand tweets refuting the original tweet. But the original story propagated out of control despite many attempts to correct it.
One of the reasons why social media exacerbates the spread of false information, or BS, as our fake news epidemic seems to suggest, is not only because of the ease of access or the speed at which salacious news can spread via such platforms:
it is also because we merely use social media and other communications platforms to do what we are hardwired to do in normal face-to-face interactions, establish and reinforce a shared worldview. Social media’s popularity does not just stem from its ability to share new information, but its ability to help users maintain and strengthen common bonds with their networks via likes, shares, and so on. These human desires are powerful forces which can lead to our flourishing when fulfilled correctly, but can also lead to tribalism and ideological fragmentation if not handled and expressed with care.
The best minds of my generation are thinking about how to make people click ads
Jeff Hammerbacher, tech entrepreneur
Not only that, social media, the internet, and smartphones are designed to draw our attention, wasting the time we could be spending thinking critically about things that matter. There have been some attempts to deal with the BS problem, such as machine learning to detect falsehoods, government regulation, and education, all of which do not seem to be particularly promising, because of technological limitations, legal limitations, and incentive limitations.
So, as with Bergstrom and West, I acknowledge that education alone will not solve the BS problem. It is, however, a modest step in the right direction, and stepping toward the right direction is the best that we can do, hence this article.
Causality
As mentioned earlier, you do not need to have expertise in data science to find BS. For any domain of knowledge production, there is often a black box in which data enters and then exits as valuable information. Oftentimes, only those inducted in that method of knowledge production have any chance of understanding how the black box works, if at all. Thankfully for us, to determine whether that information is BS, one does not necessarily need to understand the workings of the black box.
In many cases, there are problems with the data that gets fed in the box. In addition, the information that comes out can also seem implausible and therefore clue us in that something is off. Is the data that gets fed into the analysis, biased, incomplete, or irrelevant? Is the information that comes out credible? Does it corroborate with other sources?

In 2016, a pair of researchers published an article on arXiv describing their use of machine learning to identify ‘criminal’ features on the human face. The experiment was conducted in the hopes that human biases could be removed from the process of determining criminal potentiality. Concerning input, the researchers fed their black box with training sets, i.e, over a thousand images to help it distinguish between criminal and non-criminal faces.
Images of non-criminals were taken from social media while the images of criminal faces were taken from mugshots of convicted criminals provided by police departments. Already, we can discern a problem here: photos taken from social media are generally selected to present the best part of a person, while mugshots are neutral and merely used to identify criminals. A second problem is that the criminal pictures are of convicted criminals, rather than individuals who have committed crimes. These two groups do not fully overlap. And it may be that any differences identified by the machine learning black box, if any, is between non-criminals (as far as we know) and convicted criminals, rather than between individuals who have and have not committed crimes per se.
Looking now at the output, the researchers note that the black box has produced some algorithm that allows it to distinguish criminals from non-criminals with 90% accuracy: shorter distances between the corner of the eyes, smaller angles between the nose and mouth corners (θ), and a higher curvature to the upper lip (ρ). Words alone cannot convey the humour behind the above image, so an image must suffice:

The algorithm picked up smiling as a key determinant. Given that the comparison point is between social media pictures and mugshots, this difference is not surprising. What they have created is not a criminality detector but a smile detector. The above example demonstrates that in many cases, we don’t need to know how some black box works to question the information it produces. Careful analyses of the input and output data are enough to let us know that something is off.
BS proliferates partly because we like associations. When we notice associations between things, we like to tell a story about how one thing causes the other, even if no causal link exists. We are pattern seeking, and, as a heuristic, pattern seeking has merits related to our survivability in otherwise unpredictable environments. But the problem is that many things are not causally linked, even if they may be some association or correlation between them. Let us explore these ideas, i.e., correlations and causations, in turn.
Linear correlations tell us how some set of data are correlated with another set of data. If you were to plot a graph featuring the height (horizontal position) and weight (vertical position) of, for example, some football team, there will likely be a positive linear correlation between their heights and weights; that is, the heavier someone is, the more likely they will be taller. This positive result is mapped on to a correlation coefficient that goes up to 1 and down to -1. A perfect correlation would be 1, such as the relationship between proportional measurements like kilometres and meters. And a perfect negative correlation would be -1, such as the relationship between time elapsed and time left in a 90-minute football game.
A correlation coefficient of 0 means that a best-fit line through the points does not provide any useful information about how one measurement relates to the other.

The personality test known as the Eysenck Personality Inventory questionnaire measures a self-reports’ impulsivity, sociability, and neuroticism. Studies done with the questionnaire reveal that the correlation coefficient between impulsivity and neuroticism is -0.07. This means that knowing that someone has one of these traits tells you extraordinarily little about how much of the other trait they’ll have.
As we’ve all heard many times before, correlation does not imply causation. And for the most part, people who handle data, like scientists, have careful methods to draw an inference to causation from correlations. The problem is that scientists are not good at communicating these subtleties, and the popular press, motivated, as they are, to give the public a good clickable story, will exaggerate scientific findings and hint at causal relationships where there are none. ‘Drinking wine prevents heart disease,’ ‘Chocolate is good for your brain.’ You’ve read them all before.
There are typically many causal factors involved in any correlational phenomena we observe. A study once found that positive self-esteem is associated with being kissed. Now, is positive self-esteem caused by the act of being kissed, or is positive self-esteem the catalyst for being kissed? Being in a romantic relationship is strongly correlated with kissing, so maybe it’s being in a romantic relationship that is the cause for both self-esteem and being kissed. A straightforward correlational study alone will not be able to tell us which, if any, is the best explanation. Unfortunately, such uncertainties aren’t marketable.
A recent study revealed a negative correlation between fertility rate and raised house prices in America, i.e., as house prices went up, fertility rate went down. This information itself does not demonstrate that home value growth causes fertility declines, especially since only women aged 25 to 29 were looked at, and other factors like differing cultural values across states about when it’s appropriate to have children have to be taken into account. But the study was referenced by MarketWatch in an article titled: ‘Another Adverse Effect of High Home Prices: Fewer Babies.’ The word ‘effect’ implies causation when the study it cites as justification did not suggest anything to that effect.
Paying attention to language is important in this regard. Some words are obviously intended to indicate a causal relationship. Others may be more subtle. The subjunctive mood serves this purpose, as in ‘if he were a football player, he would likely be fit’.
Another problem with inferring causality is chronology. Because something comes after something else, it does not follow that the earlier thing caused the later thing. This problematic way of thinking has been identified a long time ago as an error in thinking, and hence has been given a fancy Latin name: post hoc propter hoc = ‘after this, therefore because of it.’ Here is an example of this mistake in thinking: ‘A caveman beat the wall of the cave and the sun reappeared. Therefore, beating the wall of the cave caused the sun to reappear.’ This only appears obviously false because we have background knowledge about how the planets and stars move around in the cosmos unfazed by activities on earth. But imagine how compelling this might seem to people who don’t have that knowledge and who observe, on cloudy days, how this action always leads to that phenomena.
Other ways that causality may be wrongly inferred is through data dredging. There are enough data points across time for false correlations to exist when such data sets are compared. With just one hundred dataseries, some data sets will seem very highly correlated with others. Consider this correlation between the number of deaths from anticoagulants and sociology degrees conferred in the US:

Does this imply some causal connection between these two datasets? No, because uncanny correlations like this can easily be dredged from the mountain of collected data. And based off our own background knowledge, we have no good reason to think that anticoagulants share a causal relationship with sociology degrees. So the next time you see an uncanny or implausible correlation in some sensational news article, consider the fact that this might simply be a convenient coincidence designed to sell you a false idea.
How then, can we infer probable causation from the mass of false positives? First, we should note that talk of causation deals with probabilities rather than certainties. Saying that smoking causes cancer does not mean that all smokers will develop cancer from smoking. Rather, we are saying that there are causal mechanisms in place that make it far more likely for a regular smoker to contract a form of smoking related cancer than a non-smoker. In addition to this caveat, we should also make a distinction between sufficient and necessary causes. In a sufficient cause, if A happens, B always happens; while in a necessary cause, unless A happens, B cannot happen.
For the most part, the kind of cause that the scientific enterprise can establish, especially when there are many variables involved, is probable cause. And probable cause can be ascertained through the positive manipulation of data. Let’s look at fevers. Having a moderate fever seems to be one of the body’s defences against infections. Studies show that people who have a fever, i.e., raised body temperature, are more likely to survive a bloodstream infection. This is mere correlation though. Furthermore, one could posit, with the data alone, that it’s those who are in a better condition who have fevers in the first place, and not the other way around. So how can we move from correlation to probable cause about the impact of fever on recovery rate?
We can observe data from hospitals of the recovery rate of patients who are given fever reducing drugs and patients who are not. Many such studies have shown that the former take longer to recover from viral infections. But these studies may not have randomized their treatments, and so there could be a selection bias at play: It may be the case that people who seem to be in poorer condition are given the fever reducing drugs, thus making it look like it was the drug that caused the delayed recovery when it could well have been something else.
So, one way around the selection bias problem is to completely randomise the treatments of patients and see the differences in outcome. While this may not be ethical in some contexts, other interventions for less serious afflictions and with patient consent have been deemed acceptable. This randomized approach, something that scientists consider a gold standard in research methods, produced similar results. So, at this point, we can establish that drugs that block fever slows the rate of patient recovery. But it is still not clear if it’s the temperature variance that is the cause for that difference. Rather, the difference could still be caused by unintended side-effects of the drug.
In other words, there are still two probable causes at this juncture: (1) is it the reduction of fever that is the cause of worse disease outcomes, or (2) is it the drugs themselves that have a negative impact on recovery rate? To decide between the two, scientists did the same experiment with laboratory animals but substituted the fever reducing drugs with physical cooling. Presumably, physical cooling was not something that scientists gained approval for testing on people. The studies produced similar results. Taken together, these positive manipulations of data finally provide good evidence for a causal link between fever and recovery rate.
As we can see, quite a lot of work has to be done to achieve mere probable cause. In many cases, such positive manipulations of data are not feasible, for ethical reasons or because of some other constraint. Accurate knowledge about the empirical world comes at a price: much experimentation and a willingness to change one’s mind in light of new evidence. And it is not a price that our modern quest for quick, easy, and attention-grabbing answers is willing to pay.
Numbers
Numbers have an air of objectivity to them. We think that words can be used to twist and bend the truth while numbers cannot. But numbers themselves, even when they are entirely correct, can be used to BS. They must be placed in the right context and allow for suitable comparisons for them to approach true objectivity. Outside the rarefied world of numbers in the abstract, numbers relating to complex physical phenomena are almost always estimates.
These estimates might be false or misleading if one is not careful in presenting them. For example, determining the average height of men in a certain country can be skewed if there is a selection bias from the sample chosen, and if heights are self-reported, since people tend to exaggerate their physical characteristics. Hence, this summary statistic, i.e, about the average height of men in a country or of anything else, can also be used to mislead.
Politicians could use the summary statistic to trick the public into believing that certain policies benefit them. If they say that they are cutting down on taxes and that families will save an average of $4000 year, this may mean that actual average families, families in the middle-income range, will save nothing. This is because the tax cuts may only benefit the top 1% of families who possess the lion’s share of taxable wealth. There is nothing in the above statement that indicates the average family will save $4000 a year, even though it sounds like they should.
When the late and great Carl Sagan once arrived in Washington DC late in the evening, he picked up a pack of instant cocoa in his hotel lobby. A label on the packet read: “99.9% caffeine free.” The label was clearly intended to assure consumers that their sleep would not be affected by the beverage. Relative to background information about normal caffeine content in coffee, however, Sagan had his doubts. There are about 415 milligrams of caffeine in a 20-ounce Starbucks coffee, so there is about 21 mg of caffeine per ounce. An ounce of water weighs about 28 grams, so, proportionately, 21 mg of caffeine in 28 grams of water is about 0.075%. This means that a cup of strong Starbucks coffee is also 99.9 percent caffeine free.
Sagan’s observation demonstrates the idea that the truth can be used to BS in cases when the people cannot make meaningful comparisons to background information. Other ways that the truth can be used to mislead is through the use of percentages. Looking at change through percentages can be done with numerical differences between the existing percentage points, but it can also be done through a new percentage difference between those percentage values. Our confusion between them can be used to mislead.
If we were to say that on a certain day the sales tax increases from 4 to 6 percent of the purchase price, we can represent that difference as a numerical value, i.e., increase in 2 percentage points. But we can also represent the change as an additional percentage, i.e., an increase of 50%, because 6 is 50% more than 4. So, depending on the agenda of the person or group presenting the information, they could use the difference between numerical and percentage values to make the change seem really large or really small.
Let’s consider an example of the above. A medical doctor questions the usefulness of the influenza vaccine:
In the “relatively uncommon” case where the vaccine matched the annual flu variety, the rate of influenza was 4% for the unvaccinated and 1% for the vaccinated, so 3 less people out of every 100 would become ill. In the more common scenario of vaccine/flu mis-match the corresponding numbers were 2% sick among unvaccinated [and] 1% of the vaccinated, thus 1 less person per 100.
To downplay the usefulness of vaccines, this doctor uses numerical differences in the percentage values, i.e., from 4 to 1 and 2 to 1 in the case of a vaccine match and mismatch respectively. Having done so, she then recommends her own health tonic in lieu of the influenza vaccine. But her analysis is misleading because a new percentage difference would better reflect the effectiveness of influenza vaccines. Influenza is uncommon and infrequent, and in any given population, there are going to be about only 1 to 4% who are infected. And a numerical decrease from 4 to 1% or 2 to 1% is still equivalent to a 75 to 50-percent decrease in the flu. To put these percentages in perspective, in a hypothetical population of 4 million people, about 160 thousand people would have had the flu if they were unvaccinated, and 40 thousand people would have had the flu if they were. Judging from the numbers, flu vaccines remain remarkably effective, especially when compared with an untested health tonic.
Let us move on to the next problem in quantification. The quantification of inanimate objects is relatively uncontroversial. When we measure the weights of the elements, those elements do not try to move up or down the periodic table to make themselves look better. But when we start to quantify autonomous individuals, we run into many problems. For example, when performance reviews attempt to measure the productivity of employees in a company, this attempt risks altering the behaviours they are trying to measure in ways that often undermine the validity of the measurement.
In the early 20th century, colonial Vietnam, or Indochina as it was known at the time, was rat infested. So, the authorities hired rat catchers to deal with the problem, giving them a reward for each rat tail they could present to the colonial offices. Rat tails started being delivered to the offices at exponentially higher rates, yet the rat problem seemed to be getting worse. Soon, people started seeing tailless rats scurrying around the cities. What happened was that the rat hunters would cut off the tails of their prey and leave them to reproduce so that they can collect more tails. In addition, entrepreneurial minds began to import rats from other countries and bred them so they could get a steady harvest of tails. The authorities failed to achieve their goal of eliminating the rat infestation because they structured their incentives wrong: with the prospect of reward, and with meagre evidential requirement, i.e., a rat’s tail, people naturally started gaming the system.
This phenomenon is also known as Goodhart’s Law which states that ‘when a measure becomes a target, it ceases to be a good measure.’ We see this in just about every domain that the above applies, from academic journals maximising their citation metrics so they can shoot up the ranks, to car salesmen offering huge discounts to ensure they maximise the number of cars sold, the metric by which they are judged. Psychologist Donald Campbell came up with a similar observation: ‘The more any quantitative social indicator is used for social decision-making, the more subject it will be to corruption pressures and the more apt it will be to distort and corrupt the social processes it is intended to monitor.’
Campbell used education as a related example. Assessments designed to check for evidence of learning can be valid, and even more so when the assessment is not tied – or known to be tied – to any form of visible quantitative ranking that might distort it. But when assessment scores become the sole aim of education, they lose their value as indicators that something has been learned and it may also distort teaching and learning in ways that are counterproductive. An emphasis on ‘teaching to the test’ lowers the real quality of education and produces privileged members of society who are adept at making themselves look good with quantitative metrics but who don’t possess much of the substance those metrics were designed to measure.
Unlike elements on the periodic table, people care about how they are measured, especially when those measurements are tied to resources, rewards, or recognition of some kind or other. So, if we are in a position to measure something, think about whether the measurement will change people’s behaviours in ways that undermine the validity and value of the measurement, and adjust accordingly. Even if you are unable to eliminate the measurement problem entirely, you can still craft measurements that promote the kind of behaviours you know will help the company flourish. If the measurements have already been taken, then you have to ask whether people could have gamed the system to achieve those results and don’t rely on them if so.
Mathiness is another thing to look out for. Mathiness refers to ‘formulas and expressions that may look and feel like math—even as they disregard the logical coherence and formal rigor of actual mathematics.’ In healthcare quality management, this equation pops up from time to time:

Where A: Appropriateness; O: Outcomes; S: Service; and W: Waste. This seems like a well-thought out way of thinking about patient care. But it isn’t. This is classic BS. It is designed to impress its audience with the use of an equation, which brings with it an air of rigour. But the equation makes a claim that cannot be supported by positing formal relationships between impossible to standardize and measure quantities.
The relationships between the quantities above can, in principle, be expressed on any of the following ways:
Q = A + O + S – W
Q = S x (O + A) / W
Q = (A + O) x S – W
Q = W√(A0 + S0)
What seems to matter is that A, O, and S are additive or multiplicative in some way, and W is subtractive or divisive in some way. If the creators of the equation are not able to justify why one equation should be preferred over another, then there is no reason to accept the original equation, or any other.
There is another equation, the Trust equation:

The way the above terms relate to create trust seems to be right. But the equation brings with it specific implications for how we are to measure trust. If PSI or perception of self-interest is divisive, this means that if PSI is low, then the degree of trust can become relatively large. But if there is no perception of self-interest, does that mean that trust becomes undefined? What does it mean to divide a numerator into zero parts? Try it on your calculator.
Another problem with the equation is that C, R, and A are equally additive. That means that, if, for example, R, and A are zero but C is extremely high, then trust can still be exceedingly high. Something does not seem right: does this mean that we should be very trusting of an incredibly authentic person who has zero credibility and reliability and whom we only perceive a little self-interest? These are unintended results of presenting imprecise qualitative indicators with mathematical precision to create a perception of rigour.
There is another factor to consider. Recalling dimensional analysis in your math class, the numerical ‘currency’ on both sides of an equation have to be the same for the equation to have meaning. Think of units of measurements, you cannot mix miles (distance) with hours (time). They are represented in numerals but cannot be mixed unless you intend to create a third currency, speed in the form of miles per hour. With this in mind, let’s consider one last equation, the formula for happiness:
H = S + C + V
Where S is one’s innate disposition toward happiness, C is circumstance, and V those aspects of life under voluntary control. Assuming that these are quantifiable, are they in the same currency? What is the common unit of measurement, and is that common unit the same for the left side of the equation, happiness? The creator of this equation argues that H is the mathematical sum of these quantities. This seems highly implausible. One possible way to render the equation useful – again assuming that S, C, and V are quantifiable – is to claim that H is a function of S, C and V. Even so, this is a prime example of mathiness.
Selection Bias
When Carl skied Solitude for the first time, at fifteen, he was so taken by this tendency that he mentioned it to his father as they inhaled burgers at the base lodge before taking the bus back to the city. “I think maybe I underestimated Solitude,” Carl told him. “I had a pretty good day here. There is some good tree skiing […] and I bet I didn’t even find the best runs,” Carl continued. “There must be some amazing lines here. Probably two-thirds of the people I talked to today like this place even more than Alta or Snowbird! That’s huge praise.” Carl’s father chuckled. “Why do you think they’re skiing at Solitude?” he asked.
Calling BS
This story illustrates how easy it is for us to forget the power of selection effects. If, like Carl, we surveyed people skiing at a certain place what their favourite ski spot is, we would get more people reporting that it was the present location than if we were to get a random sample of skiers from all over. But at what size can we expect a random sample to apply more broadly and reliably indicate a larger consensus? This is a question that scientists modelling the empirical world care deeply about.
When social scientists want to learn about the characteristic of some group, they typically try to poll some representative sample of said group and extrapolate their findings. They do this because it is infeasible to always gather data from every single member of the group. We can take a random sample of men in a particular country to estimate the average height of men in that country. One issue with this approach is that, if we are not careful about who we choose and how we measure, the data will be distorted in problematic ways.
If you want to sample political leanings of a certain demographic, don’t take polls only at organic farmers’ markets; you’re going to get more people with a liberal leaning. Likewise, don’t take the same polls only at gun shows; you’re going to get the opposite. Both sets of data alone will produce misleading results that are not representative of everyone under study. Consider also whether the act of sampling will alter the results, out of fear of embarrassment or concerns with privacy, for example.
It’s also important to note that the random in random sample does not have to be truly random, but only random with regard to the quality or preference that is under inquiry. Suppose we choose the first ten names of every alphabet in a phone book and asked them about their political preferences. This choice is clearly not random, but it is random with regard to political preference and hence is a valid choice of sample.
The issue of random sampling is particularly pertinent in the field of social psychology since findings published in this field purport to reveal cognitive and behavioural mechanisms that apply to all humans. The problem with much research in the social sciences is that the common subjects of study are undergraduates. These undergraduates hailing from western countries constitute what has been coined WEIRD populations: Western, Educated, Industrialised, Rich and Democratic, and they are overwhelmingly popular because they are easy to recruit at universities and cheap to hire. They are not a random sample and, in some cases, also not random with respect to the quality or preference under study.
Then there is also the observer selection effect. The very act of observation biases the data in some way. Google discovered this when they used machine learning techniques to identify their most productive employees. They discovered that job performance was negatively correlated with success in programming contests. Why should this be? While some tried to erect plausible ad hoc reasons for this, the answer lies in the fact that google employees are not a random sample of the population at large. They have already been strongly selected for programming ability, so any negative correlation with job performance can be attributed to observer selection bias.
To better understand this, we could think about another question that probably many men and women looking for a relationship have encountered and complained about: why are hot people such jerks and why are the relatively nicer people unattractive? Otherwise known as Berkson’s paradox, this observation seems to be a common refrain of the lovelorn. When someone goes on a date with an attractive person, they tend to be a jerk, and when they go on a date with a nice person, they tend to be unattractive. One common explanation is that good looking people have discovered that they can be mean and get away with it because of their looks. But there is a better explanation related to the observer selection effect.
Anyone looking for love can put potential partners on a plot, with the horizontal axis measuring niceness and vertical axis measuring attractiveness:

Hotness and niceness are basically uncorrelated. There is no reason to think that they are. But now let’s bring in the seeker. This seeker, we assume, wants to date someone who is reasonably attractive and reasonably nice, relative to themselves. For the most part, when it comes to love, people tend to know who is not worth their time, i.e., people who are too unattractive, or too much of a jerk for them. So, we can slash out the bottom left of the plot:

There is now a slight negative correlation between hotness and niceness. The hot people the seeker is willing to date is more likely to be a jerk and the nice people the seeker is willing to date is more likely to be unattractive. But wait, there’s more! We need to slash out another part of the plot because a la observer selection effect, not only is the seeker selective in his or her choice, but potential dates are also making dating decisions based on similar criteria, relative to themselves. So, unless the seeker is Henry Cavill or Gal Gadot, potential dates will have better options:
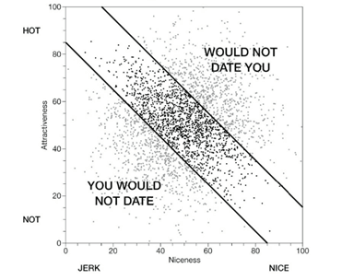
Now what is left of the dating pool bears a distinct negative correlation between hotness and niceness. And while there is no real negative correlation between these two traits among the population at large, i.e., people aren’t mean because they are hot, the universal preferences of the lovelorn (physical attractiveness and kindness are the top qualities people look for in a romantic partner, based on just about every study done) create situations where their lived experience seems to tell a different story.
So, going back to the discovery made by google about their employees, there is likely a positive correlation between programming ability and job performance in the programming job pool. But the problem is that google employees are very strongly selected for programming ability, and this means that among google employees it is no surprise that there might be some negative correlation between the above two traits.
Related to selection bias is data censoring and it is another thing that we need to pay attention to if we want to weed out BS. Data censoring occurs when a sample, which is initially selected at random, has a non-random subset removed from the final analysis, thus skewing the results. See this graph about the relative death ages of musicians based on their genres:

So, it seems that the blues are a relatively safe genre and being a hip-hop musician means that you’re probably going to die at the age of 30. Clearly something seems wrong here. The incredibly large range in age of death based on an occupation that doesn’t seem to have anything to do with mortality should make us wonder what is behind the data. When we interrogate how the data is collected, we find out that the data is right-censored: people who are still alive at the end of the study were removed as data points from the study.
Suddenly the graph begins to make sense. Relative to the blues and jazz, rap and hip hop were newer musical genres at the time of the study and therefore most of its practitioners were still alive when the study ended and therefore could not be incorporated into the results. The only ones left as data points for the study were just a handful who died prematurely.
Big Data
Machine learning and big data are all the rage now and for good reason. In traditional computer programming, you write a program that generates output from data. It is effective in certain domains but somewhat inflexible. In machine learning, you give the computer training data such that it learns on its own, and eventually, the machine learning algorithm that is created is then able to perform more complex feats of cognition.
For example, to teach a computer to distinguish between lions and tigers, you would feed the computer with training data, i.e., pictures of lions and tigers, such that it might create a neural network to tell the aforementioned difference. With this learning algorithm in place, the computer can now be used to label new data and test it. As you can imagine, these algorithms can prove useful in many areas of human industry.
But as with the criminal example in the first section of this article, we do not usually need to fully understand the inner workings of some algorithm to question its value. And in fact, for deep learning models, not even the creators can understand what their programs are doing. We just need to pay attention to the input and output data to spot problematic applications. No program can correct bad data input. Unfortunately, what is glamorous in the machine learning world is developing interesting or innovative algorithms, not carefully choosing the best representative training data.
Data in the abstract can sound objective. But data gained from the physical empirical world is full of error, human bias, and other forms of inaccuracies. Apart from bias, there is also complexity. A research team at California Pacific Medical Centre was investigating how well machine learning could detect pathologies such as pneumonia and cardiomegaly from X-ray images. The algorithm that they created with their training data performed rather well in their hospital. But the strange thing was it did not perform well elsewhere. In fact, it performed poorly. A deeper look into the algorithm revealed that the computer was not even looking at the heart or the lungs to determine the diagnosis, it was looking at the word PORTABLE on the upper right hand corner of the X-ray result.
The machine decided that this was a good indicator that the patient has pneumonia. Why? Because at CPMC, portable X-ray machines were used on severely ill patients, i.e., patients with pneumonia, who have trouble accessing the radiology department. So, the machine was not performing any valid diagnosis at all, and hence would produce severely inaccurate results if it were used to read other kinds of X-ray machine printouts.
Learning algorithms are subject to human biases. Far from eliminating them, machine learning can amplify them instead. In US criminal sentencing, algorithms currently in use identify black defendants as future criminals two times that of white defendants. Automated hiring software in some companies also preferentially select men over women. This is why policy makers have begun pushing for algorithmic transparency, so that the people behind the algorithms can be held responsible for unjust or harmful actions. The problem is that much of these algorithms are considered trade secrets and hence protected.
Another case study demonstrates some of the problems with big data. An article was published in 2009 describing how Google could predict flu outbreaks based on search terms such as fever, headache, and other flu symptoms. The predictive power of google search seemed to promise a much faster and cheaper means to track the spread of viruses than traditional epidemiological methods. The article created a lot of discussion about the power of big data and how, unlike professional epidemiologists who need years of training in public health infrastructure to trace the spread of flu across populations and intervene effectively, data scientists can do the very same thing without any training.
But by 2014 it was clear that Google’s predictions were wildly off the mark. It got bad enough for Google to stop the project and take down their Flu Trends website. Thinking about it in retrospect, there are no search terms that are perfect or even good predictors of flu. “High school basketball” was considered a top 100 predictor of flu because both flu and high school basketball peaked in the winter. Google’s suggest feature also messed up the collated search results. If we start typing something, google auto-fills suggestions based on other searches, and this may cause someone searching for some malaise unrelated to the flu to key in a relevant predictor of flu instead. This can create a growing cycle that increases the frequency of search queries in a misleading way. The bottom line is that the data cannot speak for themselves: data need a theory for them to be infused with meaning. In the case of google search, without a working theory that accurately connects search terms with real flu incidents, Google can only rely on vague correlations, that, as we now know, turned out to be too inaccurate.
Science
The progress that science has made to our understanding of the world is phenomenal. It works through trial and error and can be self-correcting if the right norms are adhered to. The problem is that knowledge about the world is hard to come by, and scientists are just like other people, with the same motivations that aren’t always altruistic.
Publishing scientific papers in journals is how scientists go about establishing their reputation and extending the field of knowledge in their areas of expertise. But recently, a replication crisis has appeared in a number of scientific fields. A 2012 report noted that only 6 of 53 cancer biology studies could be replicated in a commercial lab. Similar or even worse results were reported in social psychology journals and papers on economics.
What is the cause of this? Fraud is not an adequate answer. Cases of fraud are highly publicised and for that reason may seem pervasive. But the reality is that they are rare and therefore cannot explain why more than half of scientific studies published in reputable journals cannot be replicated. To get a better answer, we have to look at what is called a p-value.
P-values tell us how likely a pattern that a scientific study has detected arose from chance alone. Because science is in the business of figuring out the difference between signal and noise, knowing the p-value of any experiment is particularly important. An analogy would help to explain what it is. A biologist is charged with stealing some expensive paintings because a fingerprint on the recovered paintings matches his. The FBI ran his fingerprints through their database and found a match.
There is a one in ten million chance that two different fingerprints can match and the biologist does not have an alibi. So, is this a done deal? No, there are some additional things to consider. How many fingerprints are in the database? Fifty million. That means that, given a one in ten million chance that two fingerprints can match, the database will yield five false positives for every one true positive. So, when considering the culpability of the biologist, the proper probability to look at is not one-in-ten million chance that he is not the culprit, but one-in-six chance that he is, given the background information that there are fifty million fingerprints in the database.
It is the confusion between the above two probabilities that creates problems for scientists when describing the p-value to the public. When drafting research papers, scientists try to distinguish between two hypotheses: (1) the null hypothesis H0, i.e., that the results obtained were obtained via chance alone and are not significant; and (2) the alternative hypothesis, H1, that the data is not a result of chance but is significant in relation to the hypothesis being tested.
Imagine you are testing the validity of Extra Sensory Perception (ESP), and use a deck of cards to do so. There are 52 cards in a deck and 4 suits, each with 13 cards. Dealing them face down, you attempt to guess as many right suits as you can. If ESP does not exist, then by chance alone, it is likely that you will guess about 1 in 4 cards out of 52 correctly. That is 13. But after going through the whole deck, you get 19 cards of one suit correct. The p-value associated with this result encapsulates how likely you could get 19 by chance. In this case, that value is 4.3 percent. This means that there is a 4.3 percent chance that you could have gotten this result by chance alone. Moving two decimal places across, as a matter of convention, the p-value would be 0.043.
The important thing to note here is that this does not mean that we should therefore be 95.7 percent certain that H1, i.e., ESP is real, and that the H0, i.e., the result being from chance alone, is false. This would be akin to making the same mistake as thinking that there is a one in ten million chance that the biologist is not guilty. As with the biologist’s case, the probability of getting 19 right by chance is not the probability that can determine the likelihood of H1.
We are looking for the probability that something other than random chance was responsible for the score, and so H1 is not cleanly determined from the p-value alone, since there can be myriad other explanations for the 19 score outside of ESP, like (1) the deck being stacked; (2) the deck having more cards of one suit; (3) you cheating, etc. The problem is that we do not have a comprehensive list of alternatives like in the case of the biologist’s fifty million fingerprints to set a prior condition. In lieu of being able to calculate the probability of these alternative hypotheses, scientists have little choice but to represent their uncertainty as a p-value.
And so, when scientists accept and publish their p-values along with their findings, misunderstandings can occur when p-values are not communicated or represented correctly in popular news or television programs. This happened when the Higgs Boson was reported in the National Geographic soon after it was discovered in 2012 with the help of the Large Hadron Collider in Geneva. The report stated that scientists are 99 percent sure that they have discovered the Higgs Boson. This is based on the 0.01 p-value. However, as we have seen, it does not follow from the p-value that scientists are 99 percent sure the Higgs Boson exists. It only follows that the results obtained with the Large Hadron Collider has a 1 percent probability of appearing by chance even if there had been such a thing as a Higgs boson. These two claims are different.
Scientists use 0.05 as an arbitrary cut-off for statistical significance. Anything above this value would mean that the hypothesis has been nullified. Because this p-value is a publication requirement, researchers are strongly incentivised to publish ‘statistically significant’ results. No scientist wins acclaim by failing in their experiments. Unfortunately, this creates ripe ground for p-hacking. P-hacking is not outright fraud, which as mentioned, is rare. P-hacking involves adopting different statistical assumptions or playing around with sample sizes until the required p-value is met and then stopping the study to preserve it.
One clear solution to this problem is to specify what data the study will look at and how to look at it in relation to one hypothesis before commencing on the experiment. The problem is that scientists are not incentivised to do this. From a researchers’ perspective, after spending months or even years gathering data for some hypothesis, what if you turn up non-significant results? You cannot publish in any journal, let alone a reputable one. So, what do you do? Throw away the tens of thousands of funding dollars and start again? Prevent your graduate students who have been working painstakingly in the lab for years from graduating? No. You and many others would naturally default to doing everything you can to get the research published, from collecting more data until the p-value drops below 0.05 and then stopping immediately, to trying out different statistical tests until you get what you want; to even changing your hypothesis, and then publishing the positive results in a reputable journal. Having done so, you convince yourself that you made the right decision because the “experiment was bound to turn up positive results in the end.” And there you have it, the cause for myriad p-hacked studies in top journals that cannot be replicated.
Remember Goodhart’s law? Turning p-values into a target threatens to invalidate their usefulness as a measure of statistical significance. So, what can be done about this? Using meta-analytical studies to distinguish between p-hacked studies and the genuine ones as well as shoring up peer review processes seem the most promising. As we wait with bated breath for the scientific establishment to make those changes, what about us? How can we determine if a journal article is telling us something meaningful about the world?
First, we have to remind ourselves that knowledge about the physical empirical world is hard won, and that results from an experiment do not definitively tell us something true about nature. Chance is involved, as are a web of assumptions about how to set up the experiment and assess the results. Each successful study contributes a little to one hypothesis among many. And the truth value of each hypothesis is predicated on a number of converging lines of evidence from multiple studies, any of which could potentially be disconfirmed by new evidence.
Any scientific paper can be wrong. All of science is provisional and subject to change in light of new evidence. That is, paradoxically, what makes it far more successful at discovering facts about the physical empirical world than any other way of knowing. Linus Pauling, scientist and only winner of two Nobel Prizes, published papers about the structure of DNA and health benefits of vitamin C that turned out to be completely wrong. Many such dead ends line the history of the scientific enterprise.
Peer review does not guarantee that published papers are right either. Reviewers do not attempt to replicate the experiment. They merely look through the paper to ensure that the methods are reasonable and the results logically and accurately follow from them. They cannot detect every unintended mistake, much less well-concealed attempts to misrepresent the data.
The least we can do, however, is to adopt some evaluative lenses to determine a paper’s legitimacy: (1) is it written in good faith, (2) is it carried out using appropriate methodologies, and (3) is it taken seriously by the relevant scientific community? For (1) and (3), check out how well cited the article is. Check to see if the journal the article is published in is connected to a major publisher that is known to be reputable. Be sceptical of extraordinary or sensational claims in low tier or relatively unknown journals. (2) depends on the extent of your black box knowledge, so you can leave that to the peer reviewers if you have none.
This section features quite a bit of science bashing. Lest we come away thinking that science is riddled with too many problems to be taken seriously, here is a quote from Bergstrom and West which I fully resonate:
Science just plain works. […] science allows us to understand the nature of the physical world at scales far beyond what our senses evolved to detect and our minds evolved to comprehend. Equipped with this understanding, we have been able to create technologies that would seem magical to those only a few generations prior. Empirically, science is successful. Individual papers may be wrong and individual studies misreported in the popular press, but the institution as a whole is strong. We should keep this in perspective when we compare science to much of the other human knowledge—and human bullshit—that is out there.
If the scientific establishment is able to correct their incentive problem and take heed of Goodhart’s law, then science will likely be able to discover things and progress society beyond our wildest imagination.
Spotting BS
Apart from subject specific skills, what tools can we use to separate fact from fiction? We should acknowledge that communication is sales. Someone is always selling something. So, when we come across some piece of information, we can ask: who is telling me this? How do they know it? And finally, what is this person trying to sell me? These questions are second nature to us in certain contexts, like when going to a used car dealership, or when receiving unsolicited mail from a stranger requesting money, but not in others. With the advent of social media and the explosion of information confronting us – often packaged in a visually appealing way – we can sometimes forget to ask these simple questions.
Be wary of unfair comparisons. In 2018, media outlets reported a sensational research study purporting to find that airport security trays carry more germs than toilet seats. But a closer look at the study revealed that the researchers were only looking at respiratory viruses, the kind that are expelled from peoples’ mouths and noses when they cough and sneeze. Armed with this additional knowledge, it now seems obvious that security trays would have more of these kinds of germs than toilet seats: people don’t cough or sneeze on toilet seats, and toilet seats have plenty of other kinds of germs that were not under study. This unfair comparison is intended for viral shock value and omits pertinent information to do so.
The above applies to any kind of comparison, including ranked lists. Lists of any kind that are ranked can be meaningful only if the entities are directly comparable or has some translatable measure. When it comes to BS, sometimes, simple mental calculations are enough to tell us that something is not right. Use fermi estimates as a first mental intervention before deciding if it is worth devoting more time and attention to determining whether some piece of information is BS.
Avoid confirmation bias. This concept has become incredibly visible in the past decade or two. It is the tendency to only notice, believe, and share perspectives that already confirm one’s established views.
At any given time, the chief source of bullshit with which you have to contend is yourself
Neil Postman
In order to do this, consciously choose to consider multiple perspectives and hypotheses. In 2018, Roseanne Barr, a TV personality posted a racist message on Twitter. The resulting outrage on social media had Disney’s ABC network cancel her sitcom. Right after, Reuters reported that Disney’s stock had gone down by 2.5 percent as a result of the cancellation. Everyone was talking about it. But remember post hoc propter hoc. That Disney’s stock went down by 2.5 was correct, but it had actually happened before the announcement of the Roseanne cancellation in the afternoon. In fact, the entire stock market dropped that morning.
Disney generated about 55 billion USD in revenue in 2017. Roseanne’s sitcom brings in about 45 million. So how does a 0.1 percent of revenue loss lead to 2.5 percent decline in stock price? Regardless, because the phenomenon of interest was paired with a sensational event, the story seemed compelling and worth publishing.
The point is that there may be multiple possible reasons for some event occurring. It does not follow that just because something is marginally consistent with the data or intuitively correct that it is therefore a good explanation. Recall the distinction between correlation and causation. So, triangulate from multiple sources and mediums. If some factoid, statistic or data graphic has no source, do not share it with others. Skip news sources that have a reputation for sensationalizing. If you are determining the veracity of an image, use reverse image lookup to discover its source. Double check domain names of popular websites where you get information from, and use fact checking websites like Snopes, PolitiFact and FactCheck.
Calling it out
Pointing out BS to others is vital to the healthy functioning of any social group. Only people who are aligned to the truth about the world around them have any chance of long-term flourishing, in every sense of the word. But we have to be careful in how we do so. When people are confronted with their own hubris or ignorance, their reactions may not be predictable or productive. This is why people who do not filter their speech are universally more likely to be ostracised by their social groups than others. So, pointing out BS to people has to be done responsibly and appropriately, remembering that you are calling out bad ideas rather than bad people, even if the latter may be implied.
One method of calling out BS is to use thought experiments that demonstrate problems when the BS in question is taken to its logical end. Researchers have noticed that in the past few decades, women have been improving in the 100-meter dash at a faster rate than men at the Olympics. Plotting a simple graph of two straight lines along the improving times of men vis-à-vis women, the researchers predicted that women would out sprint men by 2165. This was actually reported in the news. What is the problem here? This prediction ignores the physical constraints of male and female bio-machines and assumes that a straight line best predicts change in running speed. In other words, it ignores biology.
After the publication of this research, a biostatistics professor Kenneth Rice wrote a letter adopting the aforementioned strategy to call out BS:
Sir—A. J. Tatem and colleagues calculate that women may outsprint men by the middle of the twenty-second century […]. They omit to mention, however, that (according to their analysis) a far more interesting race should occur in about 2636, when times of less than zero seconds will be recorded. In the intervening 600 years, the authors may wish to address the obvious challenges raised for both time-keeping and the teaching of basic statistics.
With a few choice words, Rice shows how assumptions in the research methods lead to ridiculous conclusions. Adopting counterexamples for which some idea cannot apply when it is supposed to will also suffice to create the same effect: if someone says that A leads to B, find a case in which A is true but B does not follow.
A useful tool for this is the null model. Biologists accept that there is a process called senescence, in which our cognitive and physical abilities decline with age. One of the co-authors of Calling BS taught a class in which he used a graph showing the declining running pace of world record holders as they age, to teach students how to spot weaknesses in an argument for senescence.

He expected to hear responses such as world record holders not being representative of runners of all types and abilities, which is true. But what he did not expect a student to mention, and had not considered himself, was that there are many more people running competitively in their 20s and 30s than in their 70s and 80s, and the more runners you sample from, the better their times will be. Given random samples, the fastest runner among 10 million runners is going to be faster than the fastest runner among ten. Hence, the decreasing pace seen in the graph could be an indicator of decreasing sample size rather than evidence for senescence.
And indeed, when the null model designed to remove the impact of age on running pace was incorporated into the graph, it produced the same result minus the senescence:

This does not mean that senescence is false, because there is other evidence for it. What it means is that the first graph is not a good argument in favour of senescence. You can use null model type thinking to determine if some pattern observed could still occur if the hypothesized causal factor is removed.
People’s perspectives are oftentimes tied to some part of their identity, and it is the identity rather than the ideas that make debunking those ideas difficult. Whether its new age healing methods, or climate scepticism, find ways to decouple bad ideas from the identity those ideas are associated with. One way to do this is to show how people can retain their sense of self or their intrinsic values even if they give up those bad ideas. On a related note, pick your battles. Some people are just so entrenched in their beliefs, likely because it forms a core part of their identity, that it would not only be infeasible but also dangerous to continue engaging with them.
Keep it simple. Sometimes the truth can be rather complicated or technical when compared with viral falsehoods. So, to fight fire with fire, oftentimes, it is best to convey the truth as clearly and simply as possible, even if some nuances have to be lost in the process. Take it offline. Few like to be called out of their BS, intentioned or no, in the presence of others. But if it is clear that the BS someone is spewing and harmful and the person spewing it is doing so to harm people, then we have a moral duty to call this out publicly.
Be pertinent. This is an incredibly important point. Calling BS is not pointing out technicalities in peoples’ speech for no good reason. Here is an example:
“It’s interesting. There are lots of birds that trick other species into raising their offspring. Cuckoos, cowbirds, honeyguides, even some ducks. But mammals never do this. I wonder why not.”
“I suspect it is because mammals don’t lay eggs. That makes it a lot harder to sneak a baby in there!”
“Well, actually […] some mammals do lay eggs. Echidnas and platypuses, collectively known as monotremes and found only in Australia and Papua New Guinea, are both oviparous.”
Spot the annoying behaviour. Apart from demonstrating no self-awareness, the last response is not calling BS for a number of reasons. The first is that the factoid pointed out is irrelevant to the issue being discussed. It does not move the discussion forward. There are some egg laying mammals, but they constitute less than 0.1 percent of all mammal species, so the objection does nothing to undermine it. The second is that calling out BS should be directed at people who are intentionally being deceptive, or whose views are otherwise harmfully wrong in some way. It is not about trying to contradict someone who is engaging in a dialogue in good faith (i.e., not trying to impress or deceive) and who may therefore not be speaking with pedantic precision.
Responses like the above are also not like calling BS because the objector does not care about the intended direction of the conversation or about protecting an audience from falsehoods, but about demonstrating intellectual prowess in a private conversation. There are other ways to flex your intelligence, like getting a PhD in a difficult discipline or writing a hard to read book, and hence no need to annoy your friends. Calling BS is speaking truth to power. It is about frustrating the attempts of those who wish to beat others over the head with sophistry for nefarious purposes. It is not about putting another speaker down in casual conversation. When calling BS, one must consider whether it is helpful to do so; demonstrate some restraint, especially when you know that nothing good will come from it.
People who engage in such behaviour, in fact, have more in common with people who BS than with people who call BS. This is because someone who BSes disregards truth in order to impress or overwhelm an audience. Likewise, someone who routinely contradicts others in casual conversations is also trying to impress or intimidate them with his or her knowledge, oftentimes without regard for truth as defined by the intended direction of the conversation. Calling BS is not about making you look smarter. It is about making others actually smarter and better able to hold true beliefs and make good decisions.
Even since minds existed, there has been BS. With the advent of scientific and algorithmic thinking, BS evolved to accommodate. Left unchecked, such BS has and will continue to have serious consequences on the integrity of science, high quality decision making and human welfare overall. Science and technology are not going to help us solve this problem since they are part of the problem. We ourselves must become more vigilant, thoughtful, and sceptical of the information we receive and share. We must reinforce the spotting and calling of new age BS in public and private education. Education should not only be about learning now to manipulate newly learned information in ever more impressive ways as a mere exercise in intelligence, it should also include the ability to discriminate good from bad applications of this newly learned information.
Intelligence can only get us so far, what we need is experience with BS detecting tools. And instead of capitulating to the time strapped ultra-competitive mindset that the economy incentivises our workplaces to be, we need to create structures that allow for expert decision makers and those who support them to slow down and think, really think carefully and comprehensively, before jumping on new-fangled bandwagons supported by fancy BS. Whenever those decisions are made, the decision makers should also make their entire process transparent so that others who are affected by those decisions can rest easy that the best, most thoughtful decisions were being made. If the decisions go south, people will also be assured that the factors leading to the decision having a bad outcome could not have been foreseen. In addition, because the entire process is made available, it can be iteratively improved to handle those unforeseen factors by any competent person or team in the company.
Nothing that you will learn in the course of your studies will be of the slightest possible use to you [thereafter], save only this, that if you work hard and intelligently you should be able to detect when a man is talking rot, and that, in my view, is the main, if not the sole, purpose of education.
John Alexander Smith, lecturer of philosophy at Oxford
To stop repeating the same mistakes, and to speed up the rate of human progress, calling BS and adjusting accordingly is poised to be the most vital skill that an individual, group, society, or nation, can possess.